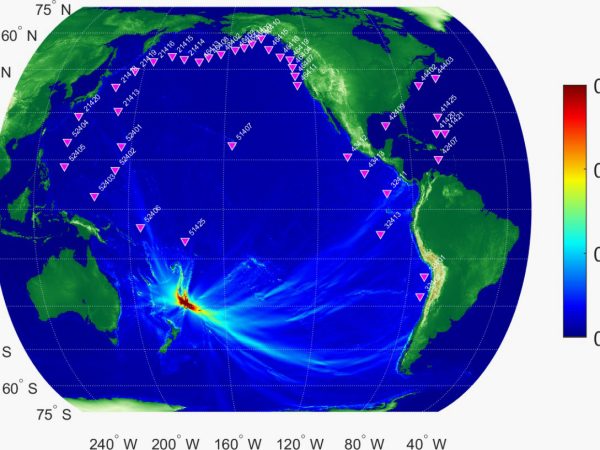
La ley de Gutemberg-Richter
Una simple y a la vez perspicaz observación que puede hacer una persona que vive en un territorio sísmico como Chile es: Hay más terremotos de magnitud baja que terremotos de magnitud alta. Es decir se perciben, en un periodo de tiempo de un año, 10 años o una vida entera, muchos más terremotos pequeños que terremotos grandes. ¿Cómo sería de otra manera? Podríamos sentir quizás un movimiento continuo del suelo bajo nuestros pies, como las olas en un lago quieto. O quizás estos movimientos tendrían una marcada periodicidad e intensidad: “aquí viene el temblor de las 5”, “ya pasó el terremoto de las 12”, podría exclamar un ciudadano atento.
El aspecto notable de esta simple observación es que al hacer una estadística cuidadosa de los números de eventos según la energía que ellos liberan se cumple una relación matemática extraordinariamente sencilla. Esta relación indica que los terremotos de baja magnitud se observan a una tasa que es exponencialmente mayor a la tasa de observación de terremotos de alta magnitud. Fue enunciada por primera vez en el año 1958 y luego denominada con el nombre de los dos sismólogos que la evidenciaron: Ley de Gutemberg-Richter.
Otra forma de expresar la ley de Gutemberg-Richter es la siguiente: el número de terremotos que liberan una energía determinada es inversamente proporcional a una potencia de esa energía. Este decrecimiento de la frecuencia de eventos observados según la energía que liberan corresponde a una relación de ley de potencia.
Las leyes de potencia aparecen no solo en la frecuencia de los eventos sísmicos, sino que también en muchos otros fenómenos tan diversos como la distribución del número de incendios forestales según el área que arrasan, el número de ciudades según el número de habitantes o el número de meteoritos según su tamaño. La presencia de leyes de potencia expresa la existencia de una simetría en el sistema: la invarianza de escala. Según esta característica las propiedades estadísticas de un sistema en una escala se relacionan a aquellas en otra escala solo a través de la razón entre ambas escalas y no a través de cualquiera de ellas individualmente.
Los modelos de terremotos basados en la mecánica clásica y en la teoría de la elasticidad han tenido éxito en representar las fuentes desde donde se producen las ondas sísmicas. Sin embargo, explicar el carácter colectivo en los terremotos y en las fallas es una tarea más esquiva para la sismología tradicional. Una perspectiva que se ha encargado de modelar la colectividad de los sistemas y sus interacciones es la de los autómatas celulares.
Un autómata celular (link wiki) es una colección de celdas “coloreadas” en una grilla de forma específica, que evoluciona en pasos discretos de acuerdo a un set de reglas basadas en el estado de celdas vecinas. Las reglas son aplicadas de manera iterativa tantas veces como se desee. Los matemáticos John Von Neumann y Stanislaw Ulam (link wiki) descubrieron este tipo de modelos en los años 1940s. Se volvieron populares en los 70’s con la divulgación de “el juego de la vida”, un autómata celular creado por John Conway que produce múltiples patrones animados a partir de reglas extremadamente sencillas. No podemos dejar de mencionar a Stephen Wolfram, quien clasificó todos los autómatas celulares de 1 dimensión y publicó el libro “Un nuevo tipo de Ciencia”, en el cual aboga por el estudio de estos programas computacionales para entender los sistemas naturales.
La pila de arena
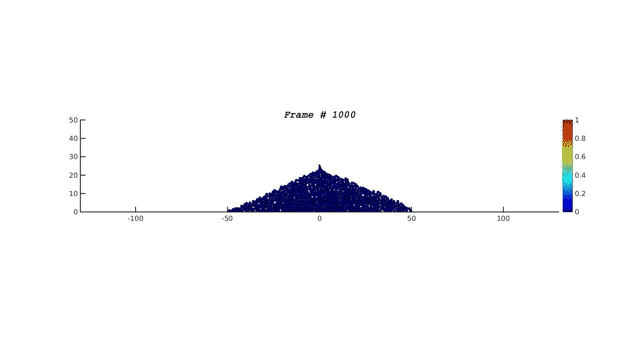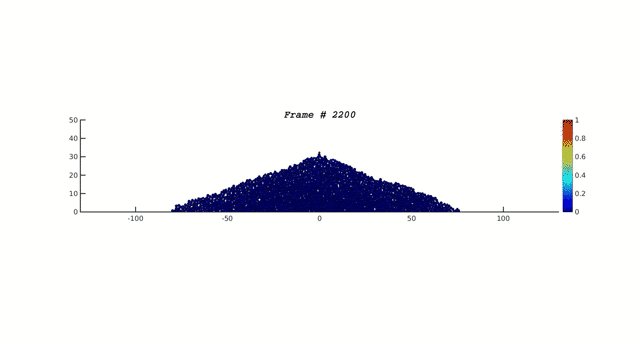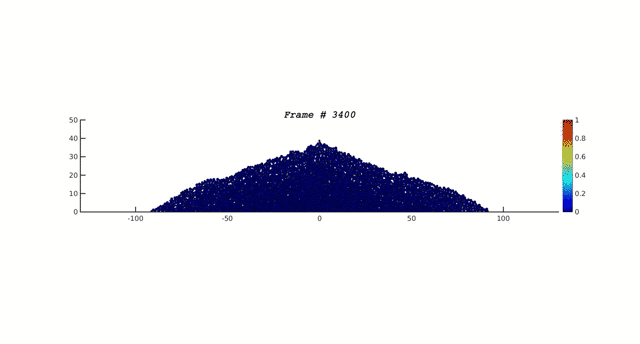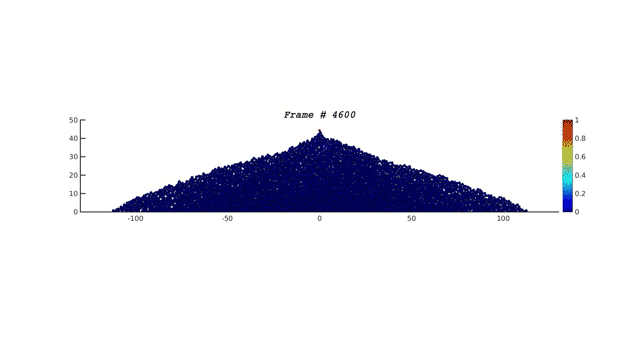
Los físicos Per Bak, Chao Tang y Kurt Wiesenfeld introdujeron en 1987 un modelo de una pila de arena que se forma al añadir continuamente granos de arena sobre una superficie. Las reglas consisten en:
- Escoge un sitio al azar
- Añade un grano de arena al sitio
- Chequea que todos los sitios tengan menos de 4 granos de arena y si se cumple, procede desde el paso 1.
- Escoge al azar uno de los sitios con 4 o más granos de arena y déjalo en cero, distribuye los 4 granos a cada uno de los vecinos más cercanos.
- Repite el paso 4 hasta que todos los sitios tengan menos de 4 granos de arena.
Los sitios con más de 4 o más granos corresponden a sitios inestables y desde ahí se producen avalanchas. Luego de cierto tiempo, la adición de un grano de arena gatilla avalanchas simultáneas en sitios vecinos. Y eventualmente el sistema llega a un estado crítico en que la adición de un grano de arena puede dejar el sistema tal cual o está o desencadenar una avalancha de larga escala. Este estado es llamado Criticalidad Auto-Organizada. El sistema evoluciona hacia un estado crítico sólo mediante la imposición de las reglas de evolución. De acuerdo a lo expuesto por Per Bak en su libro How Nature Works: The Science of Self-Organized Criticality, la criticalidad auto-organizada es el principal mecanismo que hace que emerja la complejidad observada en el universo, expresada en la existencia de leyes de potencia en fenómenos naturales. La siguiente figura (3) muestra algunas avalanchas que se producen y su analogía con los terremotos:
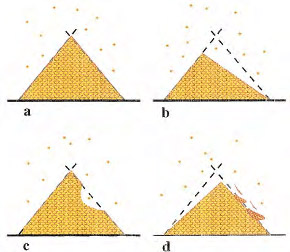
(a) Granos de arena son lentamente añadidos a la pila de arena. Todos los lados de la pila de arena llegan a un estado en el cual la adición de granos adicionales resulta en inestabilidades, es decir, avalanchas de arena de todos los tamaños.
(b) Una gran avalancha tiene lugar en una zona de la pila, dejando esa zona fuera de la criticalidad y haciendo que sea incapaz de generar avalanchas grandes por un largo periodo de tiempo (hasta que se le añadan granos de arena que lleven a la pila al ángulo crítico).
(c) Una avalancha pequeña ocurre en medio de la pila y esta no afecta a la totalidad de su lado, avalanchas pequeñas pueden aún ocurrir arriba y abajo de la zona del último derrumbe.
(d) Avalanchas de tamaño intermedio ocurren en una zona a medida que esta se acerca al estado de inestabilidad que antecede a una avalancha grande. Avalanchas grandes y pequeñas son análogos a terremotos grandes y pequeños. Figura y descripciones extraídas desde Sykes et al. (1999).
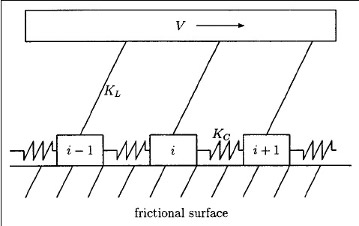
El primer modelo para representar la colectividad en el movimiento de bloques que genera los terremotos fue presentado por los sismólogos L. Knopoff y R. Burridge. Consiste en dos arreglos de bloques unidos por resortes y que se encuentran sobre una superficie rugosa y unidos mediante cables a una superficie superior. El experimento que realizaron sobre el modelo 1D recuperó la ley de G-R. En los 90’s se retomó el interés de la mano del uso de procesadores más avanzados que pudiesen resolver las ecuaciones de forma numérica. Una versión en forma de un autómata celular fue planteada por Olami, Feder y Christensen, quienes demostraron que cumple con la característica de Auto-organización en la criticalidad.
El uso de modelos computacionales en el estudio de la sismicidad ha ayudado a entender mejor el sistema litosférico donde se producen los terremotos. Esto, a su vez, ha ayudado a dirigir los esfuerzos en encontrar variables pronosticadoras de aumento de la sismicidad que puedan anteceder a terremotos destructivos. En la actualidad, el análisis de los patrones generados por los eventos sísmicos y las fallas terrestres está siendo estudiado en el PRS para establecer zonas de mayor peligrosidad sísmica sobre las cuales establecer manejos de mitigación de riesgo y una adecuada planificación territorial.